支持单字通配符的Sunday模糊匹配算法

发表于 更新于 分类于 Valine：

前言

忙碌的春节过去了（吐槽一下，现在南京不给放炮仗，真是越来越没有年味了，不但是礼炮，连擦炮、摔炮都买不到），终于能闲下来学习和写博文了。今天填一下上篇文章留下的坑。实现一个支持单字通配符的Sunday模糊匹配算法

假定需求

给定一个 haystack 字符串和一个 needle 字符串，实现一个支持 '?' 的单字通配符匹配算法。在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)，如果不存在，则返回 -1。

示例 1:

输入: haystack = "hello", needle = "l?o" 输出: 2

示例 2:

输入: haystack = "aaaaa", needle = "b?a" 输出: -1

  • 本文算法复杂度中的是模式串的长度，是主串的长度。
  • i代表主串指针，j代表模式串指针，?代表单字通配符

朴素解法（暴力匹配）

每次j向后移动1步，逐个对比，遇到?就跳过；遇到不匹配的，i向后移动1步, j再从头对比

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
public:
    int patternMatch(string haystack, string needle) {
        int h_len = haystack.size(), n_len = needle.size();
        if (!n_len)
            return 0;

        for (int i = 0; i <= h_len - n_len; ++i) { // i 主串指针
            bool found = true;
            for (int j = 0; j < n_len; ++j) { // j 模式串指针
                if (needle[j] == '?') // 遇到通配符，跳过
                    continue;
                else if (haystack[i + j] != needle[j]) { // 不匹配
                    found = false;
                    break;
                }
            }

            if (found) // 匹配，返回索引
                return i;
        }

        return -1;
    }
};

复杂度分析

  • 预处理时间复杂度：无
  • 匹配时间复杂度：
  • 空间复杂度：

Sunday解法

标准Sunday需要什么改进?

之前介绍过标准的Sunday算法是通过偏移表，在匹配失败时，确定需要移动多少，然后让i去位移

但由于?可以代表任意一个字符，所以我们无法在预处理阶段就确定需要移动多少，只能根据模式串中最后的?确定最少需要移动多少。那么我们就需要让?的偏移量动态更新

如何动态更新通配符的偏移量

每次对比中j只要遇到了?，就将偏移量更新进去。如果j从来没遇到过?，就使用通配符最小偏移。

字符偏移表和通配符偏移量如果同时存在，应该如何选择?

答案：选择字符偏移表

为什么：因为能直接将模式串和匹配的末尾字符的下一位对齐

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Solution {
public:
    int patternMatch(string haystack, string needle) {
        int h_len = haystack.size(), n_len = needle.size();
        if (!n_len)
            return 0;
            
        // 预处理
        int shift[0xFF + 1]{}; // 字符偏移表
        int wildcard_min_shitf = 0;  // 通配符最小偏移
        for (int i = 0; i < n_len; ++i) {
            if (needle[i] == '?')// 将 ? 的最小偏移量存到 wildcard_min_shitf 里
                wildcard_min_shitf = n_len - i;
            else
                shift[needle[i]] = n_len - i;
        }

        for (int i = 0; i <= h_len - n_len;) { // i 主串指针
            bool found = true;
            int step = wildcard_min_shitf; // 每次对比之前重置为最小偏移量
            for (int j = 0; j < n_len; ++j) { // j 模式串指针
                if (needle[j] == '?') // 遇到?，更新通配符偏移
                    step = n_len - j;
                else if (haystack[i + j] != needle[j]) {  // 不匹配
                    found = false;
                    break;
                }
            }

            if (found)  // 匹配，返回索引
                return i;

            // 不匹配，如果参与匹配的末尾字符的下一位在字符偏移表里，就使用字符偏移量
            if (int shift_step = shift[haystack[i + n_len]]) {
                step = shift_step; 
            }

            if (step > 0) {
                i += step;  // 出现在模式串中，按偏移量跳过
            } else {
                i += n_len + 1; // 没出现在模式串中，跳过模式串长度 + 1
            }
        }

        return -1;
    }
};

复杂度分析

  • 预处理时间复杂度：
  • 匹配时间复杂度：
    • 平均：
    • 最好：
    • 最差：
  • 空间复杂度：

实际情况测试

特征码匹配是单字通配符模糊匹配的应用场景之一

这里使用C#实现的特征码匹配对GTAV进程主模块内存进行搜索

测试环境：主串长度：将近8000万，Debug模式

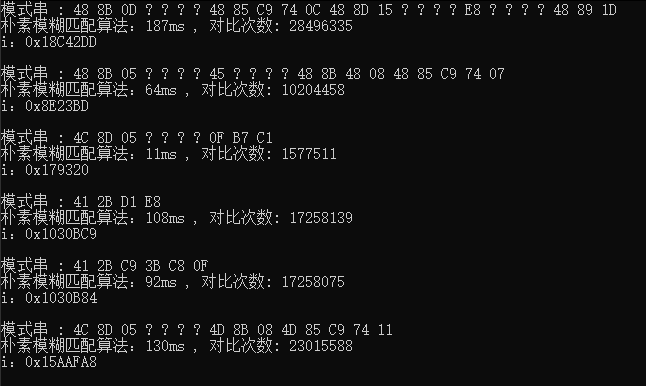
朴素算法（暴力匹配）

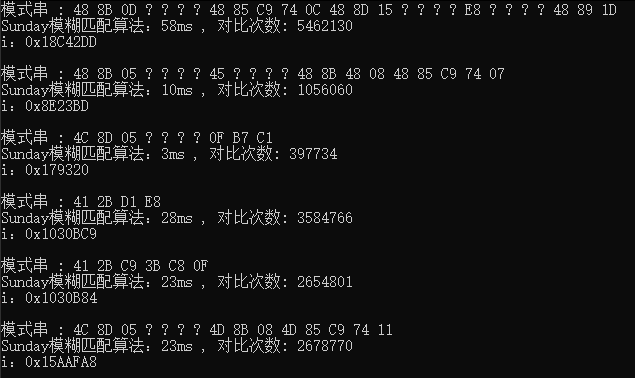
Sunday算法

总结

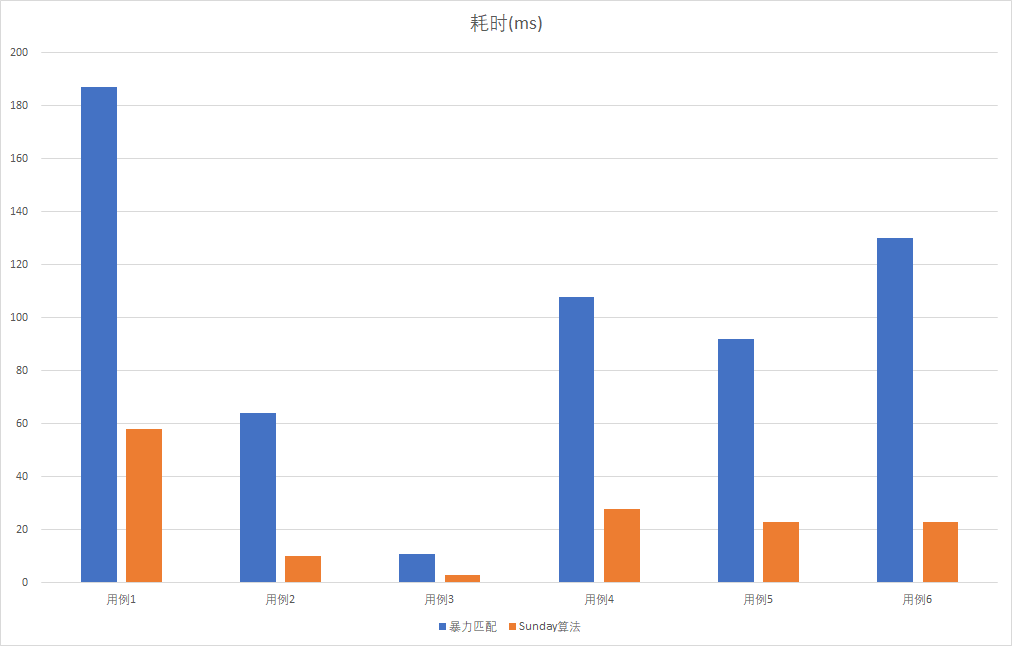
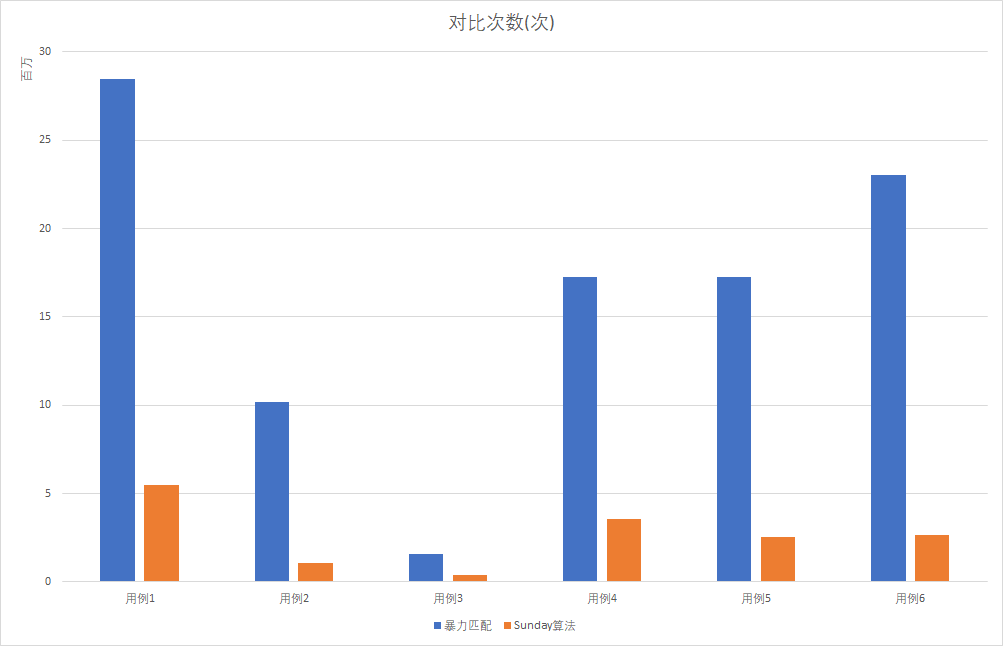
根据以上测试用例，可以看出。在特征码匹配的实际应用中，Sunday算法拥有极高的性能优势

  • 耗时：Sunday算法比朴素算法快了3-4倍
  • 对比次数：Sunday算法比朴素算法减少了4-6倍